For a project that I’m working on, I recently needed to implement an efficient dominator tree algorithm in Scala. After doing a bit of research (read: skimming the linked Wikipedia page), I decided that I should use Lengauer-Tarjan.

Usually when I need to implement a complex algorithm, I’ll do these two things, in order:

  1. Find someone else that has already done it.
  2. Failing that, actually learn the algorithm, and then implement it.

It turns out not many people make compilers or static analyzers in Scala, so option 1 didn’t seem super likely. However, I did find an implementation in Java from BinNavi, but ultimately decided against using it because I didn’t want to pull in a bunch of library files and external dependencies. The comments in the BinNavi implementation point to some pseudocode in a compiler textbook called Modern Compiler Implementation in Java, by Appel and Palsberg.

I procured a copy of said textbook and started reading the relevant sections. After understanding the theory of why the algorithm works, I got to the pseudocode listing for the algorithm itself. As I started thinking about how to implement this in Scala, I realized that the Scala implementation actually will look quite similar to the pseudocode.

In particular, by using nested defs, we can write code that looks like it modifies variables in a global namespace (as pseudocode usually does), but actually encloses them in a local namespace.

So, I started writing.

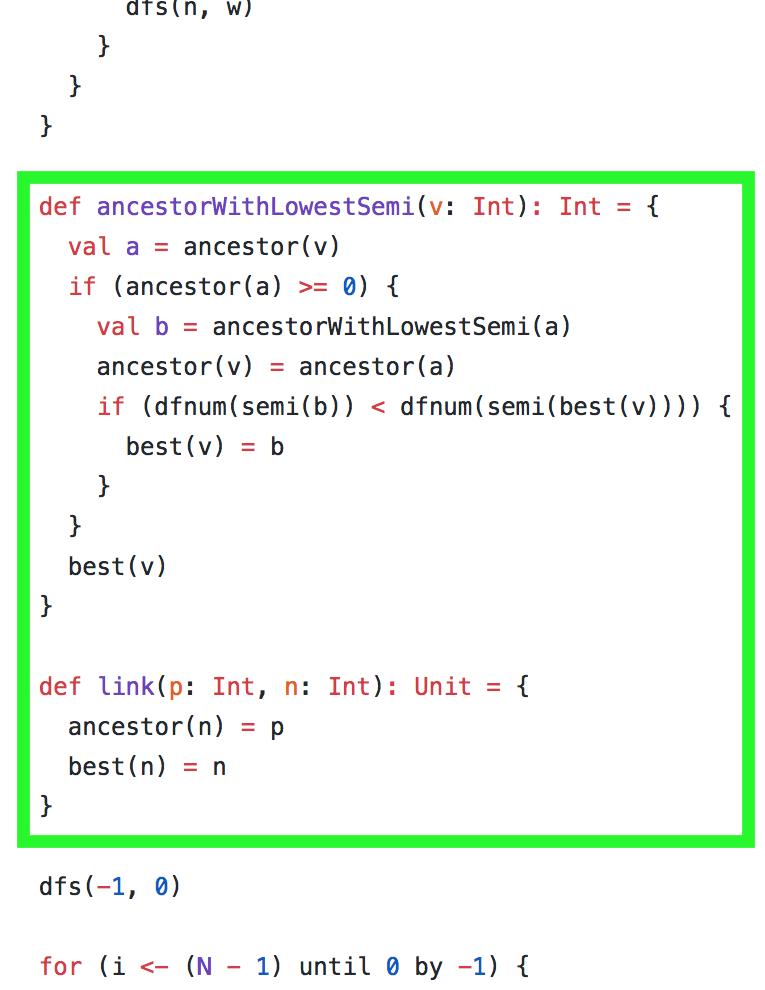Left: excerpt from Modern Compiler Implementation in Java. Right: Scala implementation.


Compare the gist to the textbook (look inside the book and search for “Lengauer”). They look really similar! I’ve highlighted above the AncestorWithLowestSemi and Link subroutines.

To be fair, you can achieve similar scoping properties in Python and JavaScript. (You can actually do this in Java as well, but you need to nest a class containing the functions that you want to nest.) But this effect is impossible to achieve in many other languages.

For completeness, here is the full Scala implementation of Lengauer-Tarjan: